2020.07.22 波形処理 第2回 平均律と純正律 (2020.08.23更新)
YouTubeでポイントを説明しています。画像をクリックすると再生できます。
波形処理第1回では音の基本となる波を、三角関数を使って作り出しました。
第2回では音程と音階を作っていきます。
音程とは、音の高さではなく、音と音との隔たりを指し、音階は音の高さにより昇順あるいは降順にならべたものです。
■ピタゴラス音律
まず最初に疑問に思うのが、1オクターブがなぜ12個の音で構成されているかです。
この起源は、ギリシャ時代のピタゴラスにまで遡ります。
ピタゴラスは一弦琴を2つ並べ、基本音とその3倍音を同時に弾くと心地よく響くことを発見しました。
ピタゴラスは基準となる音(根音)の周波数を3倍して、根音から1オクターブ内に収まるように２で割って、音を重ね合わせていきました。
これはピタゴラス音律と呼ばれ、12個の音で構成されています。
ピタゴラス音律に関しては、次回「黒鍵と白鍵」で詳しくみていきます。
音律の系譜は、ピタゴラス音律→純正律→ミーントーン→ウェル・テンペラメント→平均律と流れていきます。
■平均律
ヨーロッパで最初に平均律を2の12乗根に基づいて算出したのは数学者、物理学者であるシモン・ステヴィン（Simon Stevin、1548年 - 1620年、フランドル（現:ベルギー）ブルッヘ出身）です。
イタリアの天文学者、哲学者、物理学者であるガリレオ・ガリレイよりも早く落下の法則を発見し、また、ヨーロッパで初めて小数を提唱したとして名高く。また、力の平行四辺形の法則の発見者としても知られています。
出典: フリー百科事典『ウィキペディア（Wikipedia）』
平均律の音程では、1オクターブの中に含まれる12個の半音程をすべて等しく配置します。
つまり、音の周波数は2の12乗根を公比とする等比数列になっています。
実際の音の周波数は、(基準になる音)×2(n/12)となります。1オクターブ上の音は、2(12/12)=21=2で、基準となる音の2倍の周波数になります。
実際に、python で基準音の周波数を１として、平均律による音の周波数の比率を求めてみます。
$ vi equaltemp.py
if __name__ == '__main__':
print('1.000')
for i in range(1,13):
print('2^({0:d}/12) = {1:.3f}'.format(i,round(2**(i/12),3)))
$ python3 equaltemp.py
1.000
2^(1/12) = 1.059
2^(2/12) = 1.122
2^(3/12) = 1.189
2^(4/12) = 1.260
2^(5/12) = 1.335
2^(6/12) = 1.414
2^(7/12) = 1.498
2^(8/12) = 1.587
2^(9/12) = 1.682
2^(10/12) = 1.782
2^(11/12) = 1.888
2^(12/12) = 2.000
みてわかるように、オクターブ以外の音程に対応する周波数比は整数比にはなりません。
1つの音を鳴らす分には問題ありませんが、複数の音を同時に鳴らすと濁った音になり、平均律の音程では、きれいな音は得られません。
心地よく響く音は、基準となる音(主音)との周波数比が単純な整数比になる必要があります。
つまり、重なり合った音の、周波数比の最小公倍数が小さいほど、短い周期で同じ合成波形を繰り返し、澄んだ音になります。
澄んだ音にするには、音楽の専門家のような複雑な知識は必要ありません。
音程をできるだけ単純な整数比になるように、プログラムで比率を補正してしまいましょう。
まずは、周波数比1～2の1オクターブの範囲で分数を生成していきます。
3/2,4/3,5/3,5/4,6/4,7/4・・・
平均律の等比数列の値を、この分数で割って、1に近い値となる分数を採用します。
例えば、2^(4/12)の比率1.260を例にとると
1.260/(3/2)=0.8400
1.260/(4/3)=0.9450
1.260/(5/3)=0.7560
1.260/(5/4)=1.0080
プログラムを書くと、こんな感じになります。
$ vi justtemp.py
def ratio(target):
loop = 100
frac, denom = 3,2
error = 0.0095
while loop:
diff = abs(target*denom/frac -1)
if diff < error:
just = frac/denom;
print('{0:d}/{1:d}={2:.3f}'.format(frac,denom,just))
return
else:
frac +=1
if (frac/denom)>=2.0:
denom +=1
frac = denom + 1
loop -= 1
print('{0:d}/{1:d}'.format(frac,denom))
if __name__ == '__main__':
print('1.000')
for i in range(1,12):
hz = round(2**(i/12),3)
print('{0:.3f} '.format(hz),end="")
ratio(hz)
プログラムを実行してみます。
$ python3 justtemp.py
1.000
1.059 16/15=1.067
1.122 9/8=1.125
1.189 6/5=1.200
1.260 5/4=1.250
1.335 4/3=1.333
1.414 17/12=1.417
1.498 3/2=1.500
1.587 8/5=1.600
1.682 5/3=1.667
1.782 16/9=1.778
1.888 15/8=1.875
左側の値が平均律、真ん中が補正した整数比、右が真ん中の分数の値です。
この補正した音階は純正律音階(ツァルリーノ音階)になっていて、音階内の多くの和音が美しく響きます。
音階の構成音の周波数比を純正律音階と平均律音階で比較すると、下記のようになります。
| 平均律 |
|---|
| 1 | 1.059 | 1.122 | 1.189 | 1.260 | 1.335 | 1.414 | 1.498 | 1.587 | 1.682 | 1.782 | 1.888 |
| 純正律 |
|---|
| 1 | 1.067 | 1.125 | 1.200 | 1.250 | 1.333 | 1.417 | 1.500 | 1.600 | 1.667 | 1.778 | 1.875 |
| 1 | 16/15 | 9/8 | 6/5 | 5/4 | 4/3 | 17/12 | 3/2 | 8/5 | 5/3 | 16/9 | 15/8 |
純正律における基準となる音をドとして、ハ長調の音階に当てはめてみましょう。
| C | D | E | F | G | A | B |
|---|
| 1 | 1.125 | 1.250 | 1.333 | 1.500 | 1.667 | 1.875 |
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 |
主要3和音の周波数比をみてみると
| ド：ミ：ソ | = | 1：5/4：3/2 | = | 4：5：6 |
| ファ：ラ：ド | = | 4/3：5/3：2 | = | 4：5：6 |
| ソ：シ：レ | = | 3/2：15/8：(9/8)*2 | = | 12：15：18 = 4:5:6 |
すべての周波数比は、4:5:6と単純な比率になっています。
この中の一番高い音を1オクターブ下げた転回音程をとると、6/2=3、周波数比でいうと、4:5:3になり、ピタゴラスの定理にてでくる整数比に一致するから不思議です。
ピタゴラスの定理（三平方の定理）
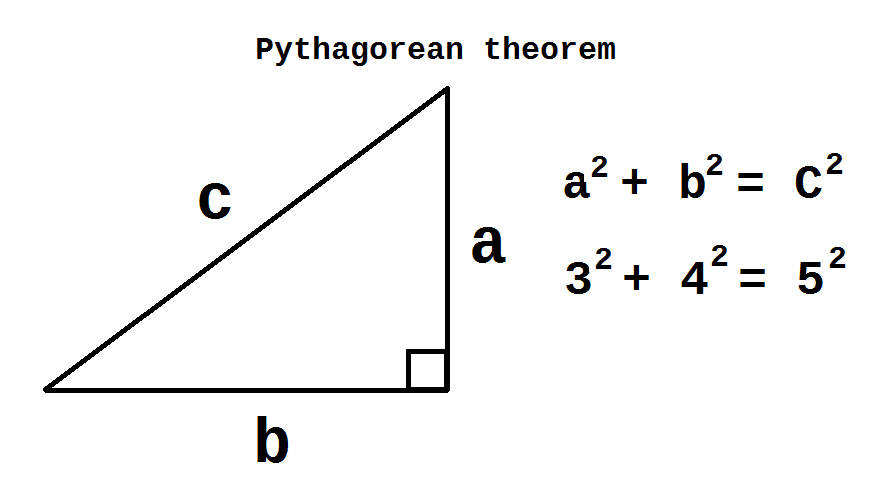
ピタゴラスの定理では、直角三角形において、斜辺の長さを c, 他の2辺の長さを a, b とすると、
a2+b2=c2 という関係が成り立ちます。
この際、a,b,c の最も簡単な整数比は a:b:c=3:4:5 となります。この均衡のとれた3,4,5という比率はとても魅力的で
さらに、aとbとcを足してできる12という数字も意味深いものに思えてきます。
ここで、1つ問題があります。
| D | E | F# | G | A | B | C# |
|---|
| 1.125 | 1.250 | 1.417 | 1.500 | 1.667 | 1.875 | 1.067 |
| 9/8 | 5/4 | 17/12 | 3/2 | 5/3 | 15/8 | 16/15 |
ドを基準音として組み立てた場合には、綺麗な周波数比になりますが、
このままの状態で、レを基準とするニ長調に適用しようととすると、二長調の主要3和音は簡単な周波数比ではなくなり、二長調の主和音は濁った響きになってしまいます。
| レ：ファ#：ラ | = | 9/8：17/12：5/3 | = | 27：34：40 |
| ソ：シ：レ | = | 3/2：15/8：(9/8)*2 | = | 12：15：18 = 4:5:6 |
| ラ：ド#：ミ | = | 5/3：(16/15)*2：(5/4)*2 | = | 100：128：150 = 50:64:75 |
このように、純正律音階は移調すると美しい響きが失われてしまいます。
これは、純正律では音階の中に、周波数比9/8と10/9の2通りの全音音程が存在することが原因です。
ド：レ＝ファ：ソ＝ラ：シ＝8：9
レ：ミ＝ソ：ラ＝9：10
コンピュータで音階を作るのであれば、ニ長調の場合は基準音をレとして、音程を配置すればよく、造作ないことですが、
生のピアノを調律する場合にはそうはいきません。
ドの音を基準に調律すると、ハ長調はきれいに響き、二長調は濁った響きになってしまいます。
平均律の利点は、音の濁りは発生するものの、すべての音程が均一なので移調は自由にできるという点です。
調律の現場では、ピアノの調律はほとんど平均律で行っているようです。
最後に周波数比4:5:6となる和音の波形を合成してみます。
$ vi chord.py
import matplotlib.pyplot as plt
import math
if __name__ == '__main__':
lcm = 16
sampling = 64
amplitude = [0]*sampling*lcm
cycle = [0]*sampling*lcm
for i in range(0,sampling*lcm):
amplitude4 = math.sin(2*math.pi*i/sampling)
amplitude5 = math.sin(2*math.pi*(5/4)*i/sampling)
amplitude6 = math.sin(2*math.pi*(3/2)*i/sampling)
amplitude[i] = amplitude4 + amplitude5 + amplitude6
cycle[i] = i/sampling
plt.plot(cycle, amplitude)
plt.show()
plt.close()
$ python3 chord.py
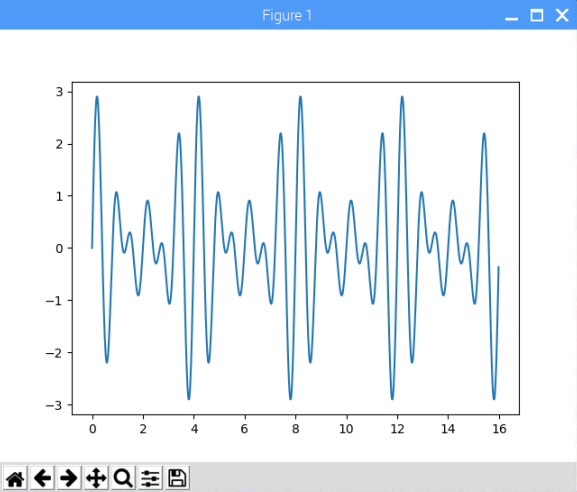
短い周期の中で、同じ波形が繰り返されているのがわかります。
今回、説明なしにいきなり、ハ長調、二長調という用語を使用してしまいました。
また、ピアノでいうところの白鍵、#の付いた黒鍵など、その成り立ちについてはまた改めて考えていきたいと思います。
■参考文献
・小林 亮 広島大学大学院理学研究科 - 音の波と三角関数
・音律と音階の科学 小方厚著 講談社
|
Raspberry Pi（ラズベリー パイ）は、ARMプロセッサを搭載したシングルボードコンピュータ。イギリスのラズベリーパイ財団によって開発されている。
たいていのことは100日あれば、うまくいく。長田英知著
「時間がなくて、なかなか自分のやりたいことができない」
「一念発起して何かを始めても、いつも三日坊主で終わってしまう」
「色んなことを先延ばしにしたまま、時間だけが過ぎていく」
そこで本書では、そんな著者が独自に開発した、
まったく新しい目標達成メソッド「100日デザイン」について、
その知識と技術を、余すところなくご紹介します。
まんがで納得ナポレオン・ヒル 思考は現実化する
OLとして雑務をこなす日々に飽き足らず、科学者だった父が残した薬品を商品化すべく、起業を決意した内山麻由(27)。彼女はセミナーで知り合った謎の女性からサポートを得ながら、彼女と二人三脚でナポレオン・ヒルの成功哲学を実践し、さまざまな問題を乗り越えていく。
ヒル博士の<ゴールデンルール>に従い、仕事に、恋に全力疾走する彼女の、成功への物語。
今日は人生最悪で最高の日 １秒で世界を変えるたったひとつの方法 ひすいこたろう著
偉人の伝記を読むと、最悪な日は、不幸な日ではなく、新しい自分が始まる日であることがわかります。最悪な出来事は、自分の人生が、想像を超えて面白くなる兆しなのです。偉人伝を読むことで、このときの不幸があったおかげで、未来にこういう幸せがくるのかと、人生を俯瞰する視線が立ち上がるのです。
ご飯は私を裏切らない heisoku著
辛い現実から目を背けて食べるご飯は、いつも美味しく幸せを届けてくれる。
29歳、中卒、恋人いない歴イコール年齢。バイト以外の職歴もなく、短期バイトを転々とする日々。ぐるぐると思索に耽るけど、ご飯を食べると幸せになれる。奇才の新鋭・heisokuが贈るリアル労働グルメ物語!
【最新版Gemini 3に対応！】できるGemini (できるシリーズ)
Geminiを「最強の知的生産パートナー」として使いこなすための、実践的なノウハウを凝縮した一冊です。
基本的な操作方法から、具体的なビジネスシーンでの活用、日々の業務を自動化するGoogle Workspaceとの連携、さらには自分だけのオリジナルAIを作成する方法まで余すところなく解説します。
Rustプログラミング完全ガイド 他言語との比較で違いが分かる!
Rustの各手法や考え方を幅広く解説！
500以上のサンプルを掲載。実行結果も確認。
全24章の包括的なチュートリアル。
ポチらせる文章術
販売サイト・ネット広告・メルマガ・ブログ・ホームページ・SNS…
全WEB媒体で効果バツグン!
カリスマコピーライターが教える「見てもらう」「買ってもらう」「共感してもらう」すべてに効くネット文章術
小型で便利な Type-C アダプター USB C オス - USB3.1 オスアダプター
Type-C端子のマイコンボードをこのアダプタを介して直接Raspberry Piに挿すことができます。ケーブルなしで便利なツールです。
Divoom Ditoo Pro ワイヤレススピーカー
15W高音質重低音/青軸キーボード/Bluetooth5.3/ピクセルアート 専用アプリ/USB接続/microSDカード
電源供給USBケーブル スリム 【5本セット】
USB電源ケーブル 5V DC電源供給ケーブル スリム 【5本セット】 電源供給 バッテリー 修理 自作 DIY 電子工作 (100cm)
|
