2020.07.22 波形処理 第2回 平均律と純正律 (2020.08.23更新)

YouTubeでポイントを説明しています。画像をクリックすると再生できます。
波形処理第1回では音の基本となる波を、三角関数を使って作り出しました。
第2回では音程と音階を作っていきます。
音程とは、音の高さではなく、音と音との隔たりを指し、音階は音の高さにより昇順あるいは降順にならべたものです。
■ピタゴラス音律
 まず最初に疑問に思うのが、1オクターブがなぜ12個の音で構成されているかです。
まず最初に疑問に思うのが、1オクターブがなぜ12個の音で構成されているかです。
この起源は、ギリシャ時代のピタゴラスにまで遡ります。
ピタゴラスは一弦琴を2つ並べ、基本音とその3倍音を同時に弾くと心地よく響くことを発見しました。
ピタゴラスは基準となる音(根音)の周波数を3倍して、根音から1オクターブ内に収まるように2で割って、音を重ね合わせていきました。
これはピタゴラス音律と呼ばれ、12個の音で構成されています。
ピタゴラス音律に関しては、次回「黒鍵と白鍵」で詳しくみていきます。
音律の系譜は、ピタゴラス音律→純正律→ミーントーン→ウェル・テンペラメント→平均律と流れていきます。
■平均律
 ヨーロッパで最初に平均律を2の12乗根に基づいて算出したのは数学者、物理学者であるシモン・ステヴィン(Simon Stevin、1548年 - 1620年、フランドル(現:ベルギー)ブルッヘ出身)です。
ヨーロッパで最初に平均律を2の12乗根に基づいて算出したのは数学者、物理学者であるシモン・ステヴィン(Simon Stevin、1548年 - 1620年、フランドル(現:ベルギー)ブルッヘ出身)です。
イタリアの天文学者、哲学者、物理学者であるガリレオ・ガリレイよりも早く落下の法則を発見し、また、ヨーロッパで初めて小数を提唱したとして名高く。また、力の平行四辺形の法則の発見者としても知られています。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
平均律の音程では、1オクターブの中に含まれる12個の半音程をすべて等しく配置します。
つまり、音の周波数は2の12乗根を公比とする等比数列になっています。
実際の音の周波数は、(基準になる音)×2(n/12)となります。1オクターブ上の音は、2(12/12)=21=2で、基準となる音の2倍の周波数になります。
実際に、python で基準音の周波数を1として、平均律による音の周波数の比率を求めてみます。
$ vi equaltemp.py
if __name__ == '__main__':
print('1.000')
for i in range(1,13):
print('2^({0:d}/12) = {1:.3f}'.format(i,round(2**(i/12),3)))
$ python3 equaltemp.py
1.000
2^(1/12) = 1.059
2^(2/12) = 1.122
2^(3/12) = 1.189
2^(4/12) = 1.260
2^(5/12) = 1.335
2^(6/12) = 1.414
2^(7/12) = 1.498
2^(8/12) = 1.587
2^(9/12) = 1.682
2^(10/12) = 1.782
2^(11/12) = 1.888
2^(12/12) = 2.000
みてわかるように、オクターブ以外の音程に対応する周波数比は整数比にはなりません。
1つの音を鳴らす分には問題ありませんが、複数の音を同時に鳴らすと濁った音になり、平均律の音程では、きれいな音は得られません。
心地よく響く音は、基準となる音(主音)との周波数比が単純な整数比になる必要があります。
つまり、重なり合った音の、周波数比の最小公倍数が小さいほど、短い周期で同じ合成波形を繰り返し、澄んだ音になります。
澄んだ音にするには、音楽の専門家のような複雑な知識は必要ありません。
音程をできるだけ単純な整数比になるように、プログラムで比率を補正してしまいましょう。
まずは、周波数比1~2の1オクターブの範囲で分数を生成していきます。
3/2,4/3,5/3,5/4,6/4,7/4・・・
平均律の等比数列の値を、この分数で割って、1に近い値となる分数を採用します。
例えば、2^(4/12)の比率1.260を例にとると
1.260/(3/2)=0.8400
1.260/(4/3)=0.9450
1.260/(5/3)=0.7560
1.260/(5/4)=1.0080
プログラムを書くと、こんな感じになります。
$ vi justtemp.py
def ratio(target):
loop = 100
frac, denom = 3,2
error = 0.0095
while loop:
diff = abs(target*denom/frac -1)
if diff < error:
just = frac/denom;
print('{0:d}/{1:d}={2:.3f}'.format(frac,denom,just))
return
else:
frac +=1
if (frac/denom)>=2.0:
denom +=1
frac = denom + 1
loop -= 1
print('{0:d}/{1:d}'.format(frac,denom))
if __name__ == '__main__':
print('1.000')
for i in range(1,12):
hz = round(2**(i/12),3)
print('{0:.3f} '.format(hz),end="")
ratio(hz)
プログラムを実行してみます。
$ python3 justtemp.py
1.000
1.059 16/15=1.067
1.122 9/8=1.125
1.189 6/5=1.200
1.260 5/4=1.250
1.335 4/3=1.333
1.414 17/12=1.417
1.498 3/2=1.500
1.587 8/5=1.600
1.682 5/3=1.667
1.782 16/9=1.778
1.888 15/8=1.875
左側の値が平均律、真ん中が補正した整数比、右が真ん中の分数の値です。
この補正した音階は純正律音階(ツァルリーノ音階)になっていて、音階内の多くの和音が美しく響きます。
音階の構成音の周波数比を純正律音階と平均律音階で比較すると、下記のようになります。
| 平均律 |
|---|
| 1 | 1.059 | 1.122 | 1.189 | 1.260 | 1.335 | 1.414 | 1.498 | 1.587 | 1.682 | 1.782 | 1.888 |
| 純正律 |
|---|
| 1 | 1.067 | 1.125 | 1.200 | 1.250 | 1.333 | 1.417 | 1.500 | 1.600 | 1.667 | 1.778 | 1.875 |
| 1 | 16/15 | 9/8 | 6/5 | 5/4 | 4/3 | 17/12 | 3/2 | 8/5 | 5/3 | 16/9 | 15/8 |
純正律における基準となる音をドとして、ハ長調の音階に当てはめてみましょう。
| C | D | E | F | G | A | B |
|---|
| 1 | 1.125 | 1.250 | 1.333 | 1.500 | 1.667 | 1.875 |
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 |
主要3和音の周波数比をみてみると
| ド:ミ:ソ | = | 1:5/4:3/2 | = | 4:5:6 |
| ファ:ラ:ド | = | 4/3:5/3:2 | = | 4:5:6 |
| ソ:シ:レ | = | 3/2:15/8:(9/8)*2 | = | 12:15:18 = 4:5:6 |
すべての周波数比は、4:5:6と単純な比率になっています。
この中の一番高い音を1オクターブ下げた転回音程をとると、6/2=3、周波数比でいうと、4:5:3になり、ピタゴラスの定理にてでくる整数比に一致するから不思議です。
ピタゴラスの定理(三平方の定理)
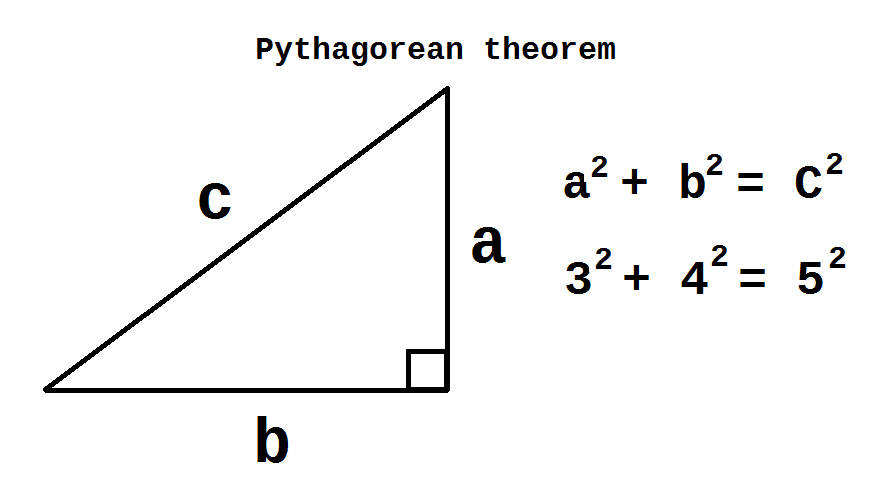
ピタゴラスの定理では、直角三角形において、斜辺の長さを c, 他の2辺の長さを a, b とすると、
a2+b2=c2 という関係が成り立ちます。
この際、a,b,c の最も簡単な整数比は a:b:c=3:4:5 となります。この均衡のとれた3,4,5という比率はとても魅力的で
さらに、aとbとcを足してできる12という数字も意味深いものに思えてきます。
ここで、1つ問題があります。
| D | E | F# | G | A | B | C# |
|---|
| 1.125 | 1.250 | 1.417 | 1.500 | 1.667 | 1.875 | 1.067 |
| 9/8 | 5/4 | 17/12 | 3/2 | 5/3 | 15/8 | 16/15 |
ドを基準音として組み立てた場合には、綺麗な周波数比になりますが、
このままの状態で、レを基準とするニ長調に適用しようととすると、二長調の主要3和音は簡単な周波数比ではなくなり、二長調の主和音は濁った響きになってしまいます。
| レ:ファ#:ラ | = | 9/8:17/12:5/3 | = | 27:34:40 |
| ソ:シ:レ | = | 3/2:15/8:(9/8)*2 | = | 12:15:18 = 4:5:6 |
| ラ:ド#:ミ | = | 5/3:(16/15)*2:(5/4)*2 | = | 100:128:150 = 50:64:75 |
このように、純正律音階は移調すると美しい響きが失われてしまいます。
これは、純正律では音階の中に、周波数比9/8と10/9の2通りの全音音程が存在することが原因です。
ド:レ=ファ:ソ=ラ:シ=8:9
レ:ミ=ソ:ラ=9:10
コンピュータで音階を作るのであれば、ニ長調の場合は基準音をレとして、音程を配置すればよく、造作ないことですが、
生のピアノを調律する場合にはそうはいきません。
ドの音を基準に調律すると、ハ長調はきれいに響き、二長調は濁った響きになってしまいます。
平均律の利点は、音の濁りは発生するものの、すべての音程が均一なので移調は自由にできるという点です。
調律の現場では、ピアノの調律はほとんど平均律で行っているようです。
最後に周波数比4:5:6となる和音の波形を合成してみます。
$ vi chord.py
import matplotlib.pyplot as plt
import math
if __name__ == '__main__':
lcm = 16
sampling = 64
amplitude = [0]*sampling*lcm
cycle = [0]*sampling*lcm
for i in range(0,sampling*lcm):
amplitude4 = math.sin(2*math.pi*i/sampling)
amplitude5 = math.sin(2*math.pi*(5/4)*i/sampling)
amplitude6 = math.sin(2*math.pi*(3/2)*i/sampling)
amplitude[i] = amplitude4 + amplitude5 + amplitude6
cycle[i] = i/sampling
plt.plot(cycle, amplitude)
plt.show()
plt.close()
$ python3 chord.py
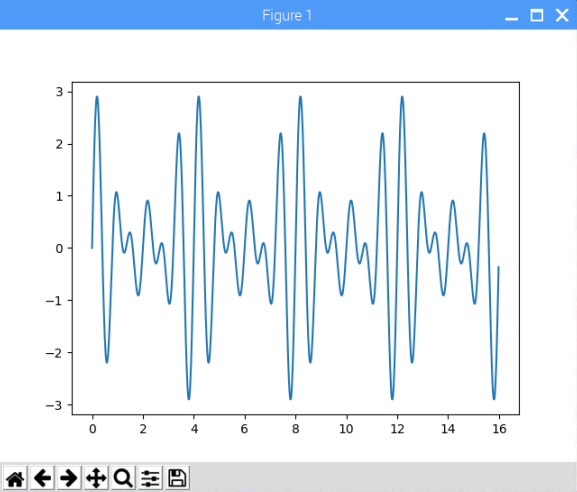
短い周期の中で、同じ波形が繰り返されているのがわかります。
今回、説明なしにいきなり、ハ長調、二長調という用語を使用してしまいました。
また、ピアノでいうところの白鍵、#の付いた黒鍵など、その成り立ちについてはまた改めて考えていきたいと思います。
■参考文献
・小林 亮 広島大学大学院理学研究科 - 音の波と三角関数
・音律と音階の科学 小方厚著 講談社
|
 Raspberry Pi(ラズベリー パイ)は、ARMプロセッサを搭載したシングルボードコンピュータ。イギリスのラズベリーパイ財団によって開発されている。
Raspberry Pi(ラズベリー パイ)は、ARMプロセッサを搭載したシングルボードコンピュータ。イギリスのラズベリーパイ財団によって開発されている。

 Arduinoで学ぶ組込みシステム入門(第2版)
Arduinoで学ぶ組込みシステム入門(第2版)
●Arduinoを使って組込みシステム開発を理解する
・ハードウェアやソフトウェアなどの基礎知識/
・設計から実装までを系統的に説明するモデルベース開発/
・Arduinoを用いた実際の開発例

 最新 使える! MATLAB 第3版
最新 使える! MATLAB 第3版
◆◆すぐに「使える!」 全ページフルカラー!◆◆
・MATLAB R2022bに対応し、解説もより詳しく!/
・コマンド・スクリプトの例が豊富で、動かして学べる!/
・超基本から解説。これから使いはじめる人にぴったり!/
・全編フルカラー、スクリーンショットも豊富!

 Amazon Web Services基礎からのネットワーク&サーバー構築改訂4版
Amazon Web Services基礎からのネットワーク&サーバー構築改訂4版
1.システム構築をインフラから始めるには/
2.ネットワークを構築する/
3.サーバーを構築する/
4.Webサーバーソフトをインストールする/
5.HTTPの動きを確認する/
6.プライベートサブネットを構築する/
7.NATを構築する/
8.DBを用いたブログシステムの構築/
9.TCP/IPによる通信の仕組みを理解する

 C言語は第二の母国語: 独学学生時代から企業内IT職人時代に培った、独立のための技術とノウハウ 平田豊著
C言語は第二の母国語: 独学学生時代から企業内IT職人時代に培った、独立のための技術とノウハウ 平田豊著
学生時代から独学でプログラミングをはじめ、企業内でデバイスドライバを開発し、そして独立後もたくさんのアプリケーション開発や技術書制作に携わってきた著者。その筆者が大事に使い続ける「C言語」の“昔と今”について、気づいたことや役立つ知識、使ってきたツールなどについて、これまで記してきたことを整理してまとめました。
本書では、現役プログラマーだけでなく、これからプログラミングを学ぶ学生などにも有益な情報やノウハウを、筆者の経験を元に紹介しています。

 1冊ですべて身につくJavaScript入門講座
1冊ですべて身につくJavaScript入門講座
・最初の一歩が踏み出せる! 初心者に寄り添うやさしい解説
・最新の技術が身につく! 今のJavaScriptの書き方・使い方
・絶対に知っておきたい! アニメーションとイベントの知識
・プログラミングの基本から実装方法まですべて学べる

 図解! Git & GitHubのツボとコツがゼッタイにわかる本
図解! Git & GitHubのツボとコツがゼッタイにわかる本
ソフトウェア開発では欠かすことのできないGit、GitHub。
これからGit、GitHubを使いたいという入門者の方でも、実際に手を動かしながら使い方を学べます。

 C自作の鉄則!2023 (日経BPパソコンベストムック)
C自作の鉄則!2023 (日経BPパソコンベストムック)
メーカー製のパソコンはスペックが中途半端で、自分が本当に欲しい機種がない――。そう思っている人には、ぜひ自作パソコンをお薦めします。自作パソコンのパーツは進化が速く、しかも驚くほど種類が豊富。価格も性能も、幅広く用意されているため、満足度100%の“自分だけの1台”を手に入れることができます。

 Interface 2023年6月号
Interface 2023年6月号
特集:第1部 フィルタ設計 基礎の基礎/
第2部 係数アプリや波形観測アプリで合点!FIR&IIRフィルタ作り/
第3部 配布プリント基板で体験!マイコンで動くフィルタ作り

 日経Linux 2023年5月号
日経Linux 2023年5月号
【特集 1】 AI時代の最強フリーソフト ~ 25のやりたいを実現!
【特集 2】 AWS、Azureのうまみを無料で体感!面倒なことはクラウドに任せよう
【特集 3】 新しいRaspberry Pi Cameraで遊んでみよう
【特集 4】 Linuxで旧型PCを復活! 1kg切るモバイルPCを「ChromeOS Flex」でChromebook化

 ラズパイマガジン2022年秋号
ラズパイマガジン2022年秋号
特集:5大人気ボード 電子工作超入門
「半導体不足で在庫が不足し、電子工作のボードがなかなか買えない…」。そんな今にふさわしい特集を企画しました。5種の人気ボードにすべて対応した電子工作の入門特集です。「GPIO」や「I2C」を使った電子パーツの制御方法は、どのボードでも同じです。手に入れられたボードを使って、今こそ電子工作を始めましょう。

 地方で稼ぐ! ITエンジニアのすすめ
地方で稼ぐ! ITエンジニアのすすめ
学歴、理系の知識、専門スキル……全部なくてもITエンジニアになれる!
地方でも高収入でやりがいをもって働ける!ITエンジニアの魅力を一挙大公開

 Raspberry Piのはじめ方2022
Raspberry Piのはじめ方2022
本書は、ラズパイやPicoの買い方やインストール、初期設定といった基本から、サーバー、電子工作、IoT、AIといったラズパイならではの活用方法まで、1冊でお届けします。
ラズパイをこれから始める方向けに、全36ページの入門マンガ「女子高生とラズベリーパイ」も巻末に掲載。これを読むだけでラズパイがどんなものなのか、すぐに分かって触れるようになります。

 ハッカーの学校 IoTハッキングの教科書
ハッカーの学校 IoTハッキングの教科書
生活にとけこみ、家電機器を便利にするIoT技術。
Webカメラなど、便利の裏側に潜むセキュリティの危険性をハッキングで検証。
専門家がパケットキャプチャからハードウェアハッキングまで、その攻撃と防御を徹底解説。
本書は2018年7月に刊行された「ハッカーの学校IoTハッキングの教科書」に一部修正を加えた第2版です。

 攻撃手法を学んで防御せよ! 押さえておくべきIoTハッキング
攻撃手法を学んで防御せよ! 押さえておくべきIoTハッキング
本書は、経済産業省から2021年4月にリリースされた、IoTセキュリティを対象とした『機器のサイバーセキュリティ確保のためのセキュリティ検証の手引き』の『別冊2 機器メーカに向けた脅威分析及びセキュリティ検証の解説書』をもとに、IoT機器の開発者や品質保証の担当者が、攻撃者の視点に立ってセキュリティ検証を実践するための手法を、事例とともに詳細に解説しました。

 ポチらせる文章術
ポチらせる文章術
販売サイト・ネット広告・メルマガ・ブログ・ホームページ・SNS…
全WEB媒体で効果バツグン!
カリスマコピーライターが教える「見てもらう」「買ってもらう」「共感してもらう」すべてに効くネット文章術

 プログラマーは世界をどう見ているのか 西村博之著
プログラマーは世界をどう見ているのか 西村博之著
イーロン・マスク(テスラ)、ジェフ・べゾス(Amazon)、ラリー・ペイジ(Google)…etc.
世界のトップはなぜプログラマーなのか?

 ニーア オートマタ PLAY ARTS改 <ヨルハ 二号 B型 DX版> PVC製 塗装済み可動フィギュア
ニーア オートマタ PLAY ARTS改 <ヨルハ 二号 B型 DX版> PVC製 塗装済み可動フィギュア
「NieR:Automata」より、ヨルハ二号B型こと2BがPLAY ARTS改に新たに登場!
高級感の感じられるコスチュームや髪の質感、洗練されたボディバランス、細かなデティールに至るまでこだわり抜かれた逸品。
DX版には通常版のラインナップに加え2Bの随行支援ユニット ポッド042などをはじめ“純白の美しい太刀"白の約定やエフェクトパーツ、自爆モードを再現できる換装用ボディパーツ、シーンに合わせて変えられる顔パーツ2種も付属する豪華な仕様に。
作中のあらゆるシーンを再現することが可能なファン必見の一品となっている。

 Newtonライト2.0 ベイズ統計
Newtonライト2.0 ベイズ統計
ベイズ統計は,結果から原因を推定する統計学です。AIや医療などの幅広い分野で応用されています。その基礎となるのは18世紀に考えだされた「ベイズの定理」です。
この本では,ベイズ統計学のきほんをやさしく紹介していきます。

 白光(HAKKO) ダイヤル式温度制御はんだ吸取器 ハンディタイプ FR301-81
白光(HAKKO) ダイヤル式温度制御はんだ吸取器 ハンディタイプ FR301-81

 無水エタノールP 500mlx2個パック(掃除)
無水エタノールP 500mlx2個パック(掃除)

 ケイバ(KEIBA) マイクロニッパー MN-A04
ケイバ(KEIBA) マイクロニッパー MN-A04

 サンハヤト SAD-101 ニューブレッドボード
サンハヤト SAD-101 ニューブレッドボード

 白光(HAKKO) HEXSOL 巻はんだ 精密プリント基板用 150g FS402-02
白光(HAKKO) HEXSOL 巻はんだ 精密プリント基板用 150g FS402-02

 [Amazon限定ブランド]【指定第2類医薬品】PHARMA CHOICE 解熱鎮痛薬 解熱鎮痛錠IP 100錠
[Amazon限定ブランド]【指定第2類医薬品】PHARMA CHOICE 解熱鎮痛薬 解熱鎮痛錠IP 100錠
|